- Forward osmosis is not dead – interview with leading water consultant Walid Khoury - August 30, 2020
- Listing of major commercial & academic FO players on ForwardOsmosisTech - April 12, 2020
- 0.26MGD FO-SWRO Hybrid for seawater desalination achieves 25% energy reduction compared to MF/SWRO - December 14, 2019
Forward osmosis, the second law of thermodynamics, and entropy
The goal of this article is to give readers a detailed introduction and explanation to the principles of forward osmosis (FO). In addition, the FO process will be explained through relevant equations, data tables, and figures.
Now, imagine a system where two compartments, holding aqueous solutions with different solute concentrations, are separated by a semi-permeable membrane, which only allows water to pass through. For the system in question, the difference in solute concentrations is spontaneously minimized by diffusion of water through the semi-permeable membrane. The direction of water diffusion is from the low concentration side to the high concentration side. This is the process of forward osmosis (FO) and the semi-permeable membrane is classified as a forward osmosis membrane (FO membrane).
The spontaneous process described above can be explained by the second law of thermodynamics, which states that the entropy (or amount of disorder) of an isolated system never decreases. This implies that isolated systems will always spontaneously evolve towards thermodynamic equilibrium – the state with maximum entropy.
Now, from a thermodynamic viewpoint the two-compartment system in question is imbalanced – one compartment contains a solution with higher solute concentration than the other – and, according to the second law of thermodynamics, it will spontaneously evolve towards a state of equilibrium where the difference in solute concentrations is minimized and the entropy is maximized.
Osmotic pressure and the forward osmosis process
The driving force for water diffusion in forward osmosis processes is quantified by the osmotic pressure ∏. In ideal solutions with low solute concentration the osmotic pressure can be approximated by the Morse equation:
∏ = iRTM
- i is The Van’t Hoff factor, which reflects the dissociation multiple of the solute species in question. For a dilute solution of sodium chloride, the Van’t Hoff factor is equal to 2 because 1 mole of NaCl dissociates into 2 moles of solutes in aqueous solution.
- R is the gas constant in L*atm*K-1*M-1
- T is the temperature of the solution in Kelvin [K]
- M is the molarity of the solution in Molar [M]
The table below summarizes osmotic pressures (in bar) of common solutions encountered in FO processes:
| Solute | Concentration in aqueous solution | Osmotic pressure |
| Mixture of ions in average seawater | N.A. | ≈28 bar |
| NaCl | 35,2 g/l | 28 bar |
| CaCl2 | 43,8 g/l | 28 bar |
| MgSO4 | 141,3 g/l | 28 bar |
| MgCl2 | 34,2 g/l | 28 bar |
Data from Achilli et. al. 2010: “Selection of inorganic-based draw solutions for forward osmosis applications”
Now let’s imagine a simple FO process in a system where two compartments with different solute concentration are separated by an ideal semi-permeable membrane, which only allows water molecules to pass through. The evolution of the system is illustrated below (figure and matching text):
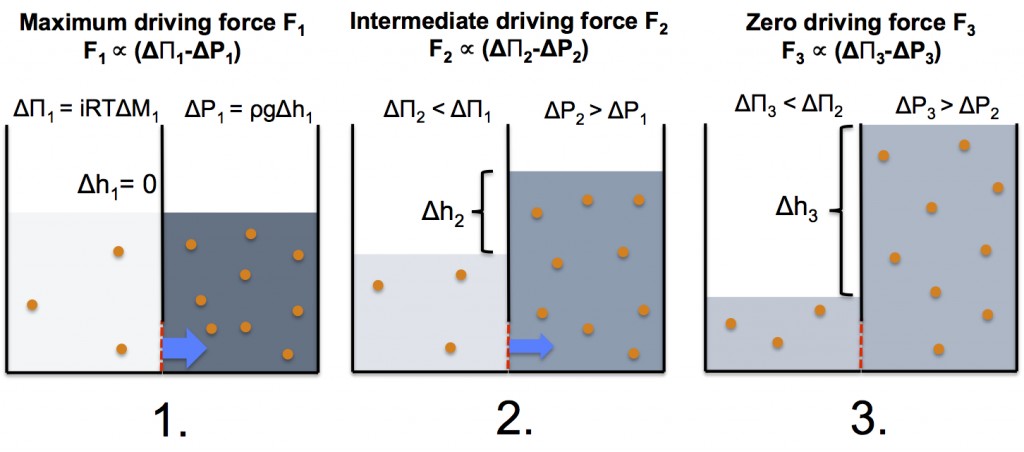
- At the starting point the osmotic pressure difference between the two compartments is largest, and since the water levels are equal, there’s no hydrostatic pressure working against the osmotic pressure. As a result, there’s a large flow of water (blue arrow) through the semi-permeable membrane (red dashed line) from the low concentration compartment to the high concentration compartment.
- At the second stage of the process, the aqueous solution in the low concentration compartment has been concentrated and the aqueous solution in the high concentration compartment has been diluted due to exchange of water from the low concentration side to the high concentration side. The change in concentrations lowers the osmotic pressure difference. In addition, the water flow into the high concentration compartment has caused an increase of the water level resulting in an opposing hydrostatic pressure. Consequently, the overall driving force has been decreased, which lowers the water flow of water across the semi-permeable membrane.
- At the third stage of the process, the osmotic pressure difference has decreased to a level where it is equal to the opposing hydrostatic pressure. As a result, the overall driving force has disappeared thus effectively stopping the water flow.
Q: Why is there a picture of a mangrove tree associated with this article?

A: Forward osmosis is the predominant method of water transport across cells of all living organisms. And root cells of mangrove trees are a great example of a naturally occurring FO process. The cells utilize a highly concentrated internal solution of sugars to extract fresh water from the surrounding seawater.


There is any International Standards or Handbooks released through Water organizations related to FO?
Hi Mohamad
First of all, thanks for reaching out! It’s always great to receive questions from our readers. To our knowledge there are no standard handbooks available.
FYI: we will soon be putting together a page on what we believe should be the standard way of testing FO membrane performance.
Cheers
Ed
What are the standards of concentrations of ions in seawater that treated by FO to be drinkable or clean enough to use by human?
Hi
whether the above Morse equation is applicable to any draw solutions?
Or this equation will be valid if we use different chemical solutions as feed and draw solution?
Hi Jinesh, to my understanding the Morse equation is independent of the draw solute molecular species. All that matters is the final amount of dissolved solutes (measured in moles).
Hence, for two inorganic salts with same Van’t Hoff factor, 1 mole of respective salt will generate the same osmotic pressure.
I hope this helps.
Kind Regards
Mark
Hi Mark
Thanks for the information
Regards
Jinesh